Crystal Structure
From Macroscopic Geometry to Atomic Arrangement
Early study of crystallography was mainly focused on the external shape and symmetry of macroscopic crystals. By carefully measuring the angles between different crystal surfaces, the symmetry, which is an important basis for crystal classification at that time, can be determined.
At the end of the 18th century, Rene Just Haüy mathematically related the macroscopic shape of crystal to its microscopic periodicity for the first time. In 1781, Haüy accidentally broke a piece of calcium carbonate crystal. Surprisingly, he discovered unexpected tiny rhombohedra from shattered crystal pieces. From this accident and proceeding systematic research of crystal cutting, Haüy concluded that “crystal” is the ordered arrangement of micro constituent molecules and developed the mathematical theory to relate them. The Haüy’s “constituent molecules” has a different notion to the modern molecules. The constituent molecules are actually micro geometrical shapes, such as parallelepipeds. Different crystals are composed of different constituent molecules.
Laue’s X-Ray diffraction experiment in 1902 is a great breakthrough in crystallography. Before this experiment, scientists could only guess what was the structure inside a crystal. Sir William Henry Bragg and Sir William Henry Bragg established the accurate analysis of the arrangement of atoms in crystal shortly after Laue’s work. The determination of structure is a prerequisite to understand physical and chemical properties of materials. For instance, understanding the crystal structure of semiconductors is the foundation to study their electrical properties. The theory of semiconductors as well as the accurate control of semiconductor processing directly lead to the birth of computer and information revolution. In addition, the structural analysis of small organic molecules and biomacromolecules by X-Ray diffraction promotes our understanding to the 3D structure of molecules. Particularly, the structural determination of biomacromolecules, such as proteins, by X-Ray diffraction technology paves a possible way for scientists to explore the secret of life.
Top diagram: silicon crystal structure.
Corpuscular theory of crystals. After Robert Hooke observed tiny crystals with regular-shaped faces under his microscope, he postulated that crystals were composed of identical spherical corpuscles. The ordered arrangement of these spheres gave rise to regular crystal faces. For example, three spheres can form equilateral triangles, while four can form rhombuses, and five can form isosceles trapezoids. Hooke also claimed that four spheres can form a tetrahedron, but he did not describe other possible three-dimensional structures. Wollaston further developed Hooke’s theory. In a paper published in 1897, he analyzed the packing of spherical, ellipsoidal corpuscles, and corpuscles with different sizes (i.e. structures on the left) . [Figure reference: Hooke, R. Micrographia (1665). Wollaston, W. H. Philos. Trans. R. Soc. Lond. 8, 527 (1897)]
Haüy’s theory of crystals. Haüy is recognized as the father of modern crystallography. He believes that crystals are made up of orderly arranged “integrant molecules” and different crystals should have different “integrant molecules”. Haüy’s integrant molecule is similar to the concept of unit cell in crystallography. Using his laws of decrement, he explained why the same crystal could occur in different geometries. For example, a cube-shaped crystal with cubic integrant molecules (green color in the above figure) can be transformed to a dodecahedral crystal with rhombic faces. To do this, we can add new layers of integrant molecules on each surface of the cubic crystal (gray color in the above figure) but each time diminish one line of molecules from each side. If we just diminish one molecule for two opposite sides while diminish two molecules for the other two sides when each time we overlay a layer of integrant molecules, the cubic crystal will be transformed to a dodecahedral crystal with pentagonal faces (not an orthogonal dodecahedron). In fact, Haüy’s laws were very advanced at that time and tightly connected to the lattice planes in modern crystallography. [Figure reference: Haüy, R. J. Traité de Minéralogie (1801)]
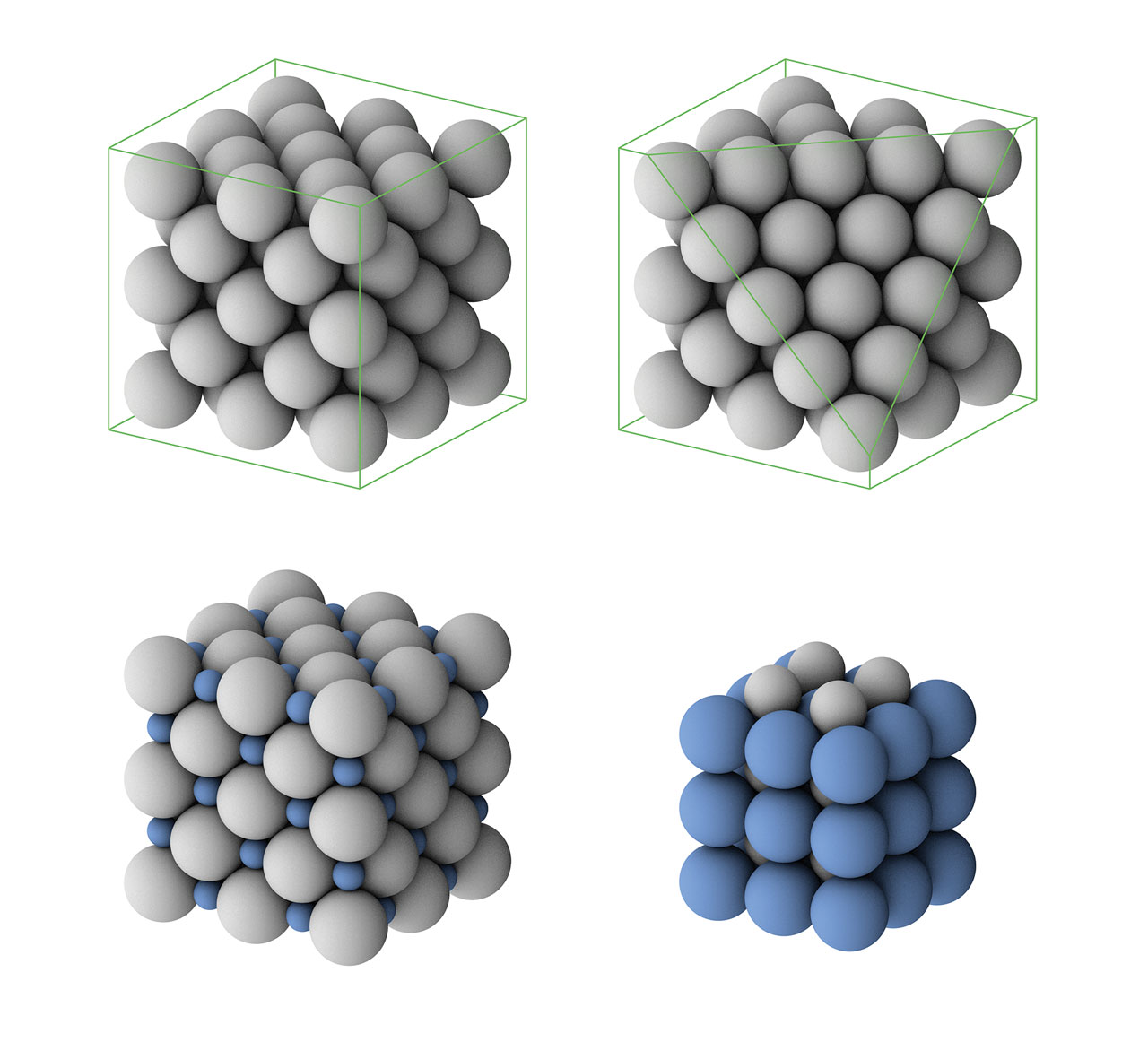
Top row: one type of close-packed structure of equal spheres.
Bottom row: crystal structures similar to sodium chloride (left) and to cesium chloride (right).
Barlow’s prediction of crystal structures. Scientists predicted some possible crystal structures before the invention of X-ray diffraction method. One good example as a series of crystal structures published by Barlow in 1897. For a crystal that only consisted of one type of atoms, he regarded all atoms as solid spheres. As a result, the crystal structure was equivalent to the closest packing of such solid spheres. (There are actually two types of closest packing but only one of them is shown in the above figure.) Barlow further analyzed the closest packing of two types of spheres and correctly predicted the structures similar as NaCl and CsCl. [Figure reference: Barlow, W. Sci. Proc. R. Dublin Soc. 103, 51 (1897)]
Laue’s crystal diffraction experiment. In 1912, 17 years after Roentgen discovered X-ray, von Laue suddenly came up with a splendid idea. He wondered if diffraction would occur when a beam of X-ray pass through a crystal since the characteristic wavelength of X-ray is close to the spacing between atoms in a crystal. In a couple of months, he proved this assumption with the help of two excellent experimentalists and they acquired the first photo of X-ray diffraction. The upper left image illustrates the X-ray diffraction photo of sphalerite took by Laue and his colleagues in 1912. Laue’s experiment not only validated the electromagnetic nature of X-Ray, but provided a powerful tool for scientist to study the microscopic structures as well. Einstein highly appraised X-ray diffraction as one the greatest physics experiments. Due to his great contribution in X-Ray diffraction, Laue received Noble Prize in physics in 1914. [Figure reference: Thomas, J. M. Nature 491, 186 (2012)]
Bragg’s equation. Although Laue’s X-Ray diffraction experiment triggered great interests in academia, it was W. H. Bragg and his son, W. L. Bragg, who successfully explained Laue’s results and made great contributions the X-ray diffraction experiments. Laue incorrectly interpreted the diffracted X-ray as an excitation consequence when the incident X-ray interacted with the crystal. However, W. H. Bragg and W. L. Bragg realized that the diffraction was actually a result of reflection of X-ray from certain crystal planes and the spacing between these planes should satisfy the famous Bragg’s equation. According to this principle, they changed the configuration of the apparatus from transmission to reflection. Therefore, solving a crystal structure finally became a reality with their contributions and the structural analysis of NaCl and diamond were very significant results at that time. Afterwards, the X-ray diffraction technology was developed rapidly. Scientist now can use it to solve the structures of inorganic materials, organic molecules, DNA, and proteins (We will see the related applications later in this book). The bottom left figure is an illustration in “X Rays and Crystal Structure”, which provided the theoretical positions of Laue diffraction spots for a piece of NaCl crystal. [Figure reference: Bragg, W. H. and Bragg, W. L. X Rays and Crystal Structure (1915)]
Top left: edge dislocation, top right: crystal plane schematic of edge dislocation, bottom left: screw dislocation, bottom right: crystal plane schematic of screw dislocation.
Dislocation. There are always a variety of defects in crystal structures. We will introduce one type of defects, dislocation, which includes two basic types: edge dislocation and screw dislocation. The concept of dislocation was firstly suggested by Tyler et al. in 1934. In 1956, Hirsch et al. confirmed the existence of dislocation by the means of transmission electron microscopy. The mechanical properties of metal are affected to dislocations. When plastic deformation applied to metals, new dislocations are generated and the gliding of dislocations occurs. In addition, screw dislocations influence crystal growth and cause the helical structure that could be observed under a microscope. [Figure reference: Read, W. T. Dislocations in Crystals (1953)]
Quasicrystals. In 1982, D. Shechtman observed a diffraction pattern that he hardly believed when he was using electron diffraction to study a fast quenched Al-Mn alloy (above image). The spots were as clear as the diffraction spots from crystals, but what confused him was the decagonal symmetry, which was impossible for crystals. Shechtman immediately realized that this pattern should imply a totally new solid structure, ordered but not periodic, and which was why it still generated clear diffraction patterns. Shechtman published the result in 1984. Scientist named this type of material “quasicrystals” and realized its similarity to Penrose pattern (p100). The discovery of quasicrystals triggered intense debates in academia. Many scientists, including L. Pauling, the two-time Nobel Laureate, denied its existence. He criticized that “No quasicrystals but only quasi-scientists.” However, more and more quasicrystals were discovered. In 1992, the International Union of Crystallography revised the definition of crystals and included the quasicrystal into the new definition. In 2011, Shechtman received Nobel Prize in chemistry for his contribution in quasicrystals. The establishment of quasicrystal is a typical example of a new idea challenging old ideas in the history of science. [Figure reference: Shechtman, D. et al. Phys. Rev. Lett. 53, 1951 (1984)]
Other Topics